株やFXでよく使われるインジケータのRSIには2種類の計算方法があります。
WilderのRSIとCutlerのRSIです。
2つのRSI
RSIはもともと、J. Welles Wilder が1978年に発表したものです。
その後、Culterはその計算を簡略化して計算しやすく、分かりやすいものにしました。
どのような違いがあるのか、例として
Cutler RSIのほうが、Wilder RSIよりも数値が極端に上下しやすい
また、急落後に全戻しのケースでは
- Wilder RSI : 50 -> 30 下落して元に戻る
- Cutler RSI : 40 -> 20 下落して元に戻る
これは同じようなうごきですがその後、
- Wilder RSI : 問題なし
- Cutler RSI : 不自然なピークが出る
このようなことが計算式の簡易化で起きることを理解して使う必要があるでしょう
以下、もう少し詳しく見てみたいと思います
Wilder(ワイルダー)のRSI と Cutler(カトラー)のRSI
Cutler RSI
Culterの計算式は簡単で計算しやすく、分かりやすいです。
A = n期間の平均上昇幅
B = n期間の平均下降幅
RSI = A / (A + B) x 100 [%]
上昇下降の平均ですが、実際の計算ではn期間の総合計で済みます。エクセルでも簡単にできます。
Wilder RSI
Wilderの計算式は、
A = n期間の平均上昇幅
B = n期間の平均下降幅
最初の1本目のRSIは、
RSI = A / (A + B) x 100 [%]
2本目以降は、
RSI = A’ / (A’ + B’) x 100 [%]
A’ = (前の平均上昇幅 x (n-1) + 今回の上昇幅) / n期間
B’ = (前の平均下降幅 x (n-1) + 今回の下降幅) / n期間
* 上昇幅で今回が前回比マイナスの場合は0とする
下降幅が前回比でプラスの場合は0とする
* Wilder はn期間を14(あるいは9)を推奨していますが、当時と現在では社会情勢が異なるので必ずとは言えないかもしれません。
* 前の平均上昇幅とは1つ前のA’であり、前の平均下降幅は1つ前のB’に相当
2本目以降では直近の動きに比重を置いているのでCutlerのような単純平均とは異なる修正移動平均となります。
Wilder氏は理系だったそうで、計算式は難しく書かれています。
RSI = 100 – (100 / (RS + 1))
RSは先のA/B あるいはA’/B’を指します。これを分かりやすくすると
RSI = (100 x (RS + 1) – 100) / (RS + 1)
= (100 x RS) / (RS + 1)
= (A/B x 100) / (A/B + 1)
= A / (A + B) x 100
となります。
WilderはRSI以外にATR、ADX、Pivotなどのインジケータの開発者です。このRSIは以下の本でで紹介されたものです。
「PR]

ワイルダーのテクニカル分析入門 ——オシレーターの売買シグナルによるトレード実践法
Wilder RSIの計算
計算式だけでは分かりにくいので簡単な例で計算してみます。エクセルを使った例は他にもあるのですが、簡単なCutler RSIが多いようです。
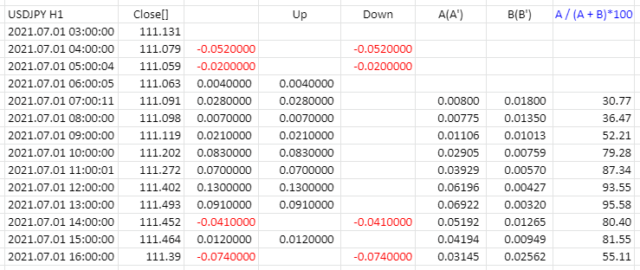
これはUSDJPYの1時間足で、Wilder RSIの期間を分かりやすく4とした場合の例です。
事前の作業として各足の終値を取り出します。
MT4の場合は「ツール」「ヒストリーセンター」からCSVファイルとして出力が可能
Close[]:前の終値と比較して差分を出します。
Up, Down:上昇したか下降したかを判断して分けます。
A: n期間の平均上昇幅、nは4にしたのでupから4つ分を加算して4で割り平均、下降したところは0としてスキップ
具体的には、(0+0+0.004+0.028)/4=0.008
B: n期間の平均下降幅、downから4つ分を加算して4で割り平均、上昇したところは0としてスキップ
具体的には、(0.052+0.02+0+0)/4=0.018
AとBが算出されたので、最初の1本目のRSIは
RSI = A / (A + B) x 100 [
30.77
Cutler RSI はこれを繰り返すだけの単純な移動平均です。
Wilder RSI は2本目から修正移動平均、一種の指数平滑になり、
A’: (前の平均上昇幅 x (n-1) + 今回の上昇幅) / n期間
具体的には、(0.00800 x 3 + 0.0070000)/4 = 0.00775
B’:(前の平均下降幅 x (n-1) + 今回の下降幅) / n期間
具体的には、(0.01800 x 3 + 0)/4 = 0.01350
RSI = A’ / (A’ + B’) x 100[ 36.47% となります。
2本目以降の計算は、SMAとEMAの違いと似ていて、
- より直近の値に比重が置かれる
- 期間以前の値が薄く加算され影響される
- 例えば期間から前のデータを変更が最新の結果に反映されるのがわかります
- また計算のスタートが異なるとRSIの値も微妙に違います
という特徴があります。
Wilder RSI 、 Cutler RSI の違い
手書きでRSIを計算するならCutlerのRSIが楽でいいのですが、今は簡単にプログラムでできしてしまいます。いずれにしても両者の違いを理解しておきましょう。
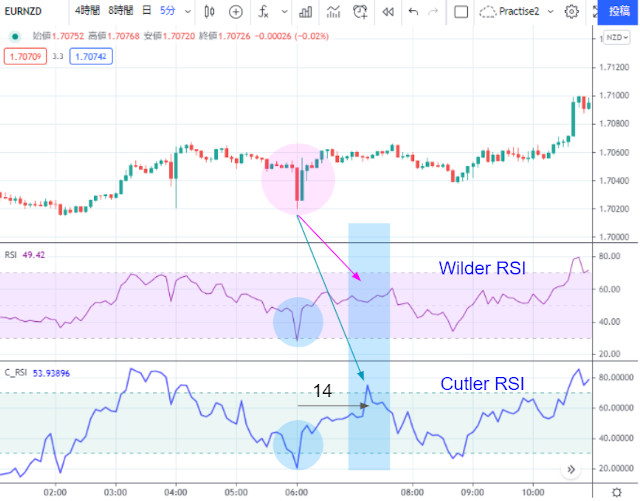
例として、EURNZDの5分足をTradingViewで表示させ、2つのRSIを表示させました。
両者とも平均は14期間とし、レベルを30~70%で見ています。

6:00に大きな下落と戻しがありました。両者ともすぐに反応していますが、
Cutler RSIはその後14期間後に不自然なピークが現れます
これは期間を14としている計算式からでるもので、SMA(単純移動平均線)とEMA(指数平滑移動平均線)の比較でもSMAに現象は同様の現象がみられます
4:00頃にも似たような下落でその14期間後に反応していますが、これらはCutlerの計算から出る問題点です。単純平均なので下落と上昇は期間内では相殺され、片方が14期間から外れると大きなピークとなってしまったわけです。
Wilder RSIは直近の動きに比重がおかれて平滑化されています。
- Cutler RSI 単純移動平均
- Wilder RSI 修正移動平均
Cutler RSIは変化に敏感だがその分ダマシにもあいそうだと言えそうです。
カーブの形はどちらも似ているがレベルは差がある
- 30
尚、TradingViewにはCutler RSIはインジケータに見当たらなかったので(その後リストに出てきたようですが)自分でPineスクリプトで書いてみました。
ダウンロードして使いたい方はこちらからどうぞ
CutlerRSI
References:
Relative strength index – Wikipedia
[PR]

ワイルダーのテクニカル分析入門
[PR]

真・チャート分析大全
小次郎講師がテクニカル指標を計算式から学ぼうというものです
Kindleに入れておけばスマホでもPCでも勉強できます